Relation Reflexiv Symmetrisch Transitiv Beispiele | Beispiel 2.man verzichtet man auf ringpfeile (reflexivität) und schreibt stattdessen unter das diagramm, ob die relation reflexiv oder antireflexiv. Wie schreibt man a steht in einer relation zu b? Eigenschaft besitzt aber nicht transitiv ist. Diese beziehung ist die art und weise, in der zwei dinge assoziiert werden können, während reflexiv ein reflexivpronomen ist. B a c d e alle personen mit.
12 12 beispiel für symmetrie die für länder definierte relation x grenzt an y ist symmetrisch. Eine relation, die reflexiv, symmetrisch und transitiv ist. 9 monate, 2 wochen her. Dann folgt aus der transitivität der beziehung ist älter als. Wir zeigen, dass die relation nicht reflexiv, symmetrisch oder transitiv ist.

Als substantive der unterschied zwischen relation und reflexion. Check for each r which is reflexiv symmetrisch transitiv ? Eine relation ist transitiv (übertragbar), wenn ∀(x,y,z)∈m: Die reflexive, symmetrische oder transitive huelle einer relation $r$ ist jene minimalste relation $r'$, die uebermenge von $r$ ist und reflexiv, symmetrisch oder transitiv (einzeln) ist. Eine relation ist allgemein eine beziehung, die zwischen dingen bestehen kann. Reflexiv, symmetrisch, antisymmetrisch und transitiv. Jedes objekt der menge ist zu sich selbst äquivalent, d. 1 ist kein direkter nachfolger von 1. Das ding ist symmetrisch und transitiv, aber nicht reflexiv da (3,3) gar nicht drin ist. Geben sie einen ausführlichen beweis oder finden sie ein beispiel einer relation r, die o.g. R:= { (1,1), (2,2), (3,3).}. Beispiel für eine transitive relation (sternzeichen). Sind folgende aussagen wahr oder falsch?
Eine relation ist symmetrisch, wenn ∀(x,y)∈m: Sei r eine symmetrische und transitive partielle relation auf einer menge a. Eine relation ist allgemein eine beziehung, die zwischen dingen bestehen kann. Am einfachsten begreiflich machen kann man die reflexivität mit einem einfachen beispiel. Beispiel für eine transitive relation (sternzeichen).
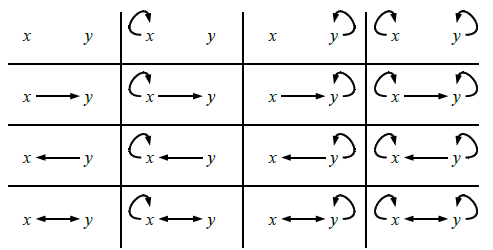
Die reflexive, symmetrische oder transitive huelle einer relation $r$ ist jene minimalste relation $r'$, die uebermenge von $r$ ist und reflexiv, symmetrisch oder transitiv (einzeln) ist. A ≥ b ∧ b ≥ a ⇒ a = b. Bei reflexiven relationen stehen also die elemente mit sich selbst in beziehung; Da ist ein adjektiv reflexiv. Beispiel 2.man verzichtet man auf ringpfeile (reflexivität) und schreibt stattdessen unter das diagramm, ob die relation reflexiv oder antireflexiv. 12 12 beispiel für symmetrie die für länder definierte relation x grenzt an y ist symmetrisch. Eine binäre relation r ⊆ s × s ist symmetrisch, wenn aus xry auf yrx geschlossen werden kann Eine relation r von m nach n ist genau dann eine funktion, wenn …. Dann folgt aus der transitivität der beziehung ist älter als. Jedes objekt der menge ist zu sich selbst äquivalent, d. Wie schreibt man a steht in einer relation zu b? Beispiel für eine transitive relation (sternzeichen). 9 monate, 2 wochen her.
Ist das jetzt reflexiv, transitiv oder symmetrisch und vorallem warum? Das ding ist symmetrisch und transitiv, aber nicht reflexiv da (3,3) gar nicht drin ist. R:= { (1,1), (2,2), (3,3).}. Die reflexive, symmetrische oder transitive huelle einer relation $r$ ist jene minimalste relation $r'$, die uebermenge von $r$ ist und reflexiv, symmetrisch oder transitiv (einzeln) ist. Ist reflexiv, symmetrisch und transitiv.
Dann gilt offensichtlich xry => yrx wegen der symmetrie von r. Relation reflexiv symmetrisch transitiv beispiele. Danke an alle, die mir weiter helfen können!!! Eine relation heißt äquivalenzrelation, wenn sie reflexiv, symmetrisch und transitiv ist. Sei m die menge der menschen und die relation ist elternteil von auf m. Dazu reicht es ein gegenbeispiel anzugeben. Ist reflexiv, symmetrisch und transitiv. Xry ∧ yrz ⇒ xrz. Die relation x ist bei facebook befreundet mit y ist ein schlechtes beispiel, weil die freundschaft bei facebook nicht zwangsläufig ist, sondern von den jeweiligen benutzern. R:= { (1,1), (2,2), (3,3).}. Wann reflexiv, wann symmetisch/antisymmetrisch, wann transitiv? Das objekt x ist äquivalent zu y. Da ist ein adjektiv reflexiv.
Relation Reflexiv Symmetrisch Transitiv Beispiele: Also steht 1 nicht in relation zu 1.
0 comments: